Spatial Relation Algorithm in GEOS

GIS 또는 Spatial database에서는 2개의 geometry 객체 (또는 spatial 객체)사이의 관계가 중요한 요소다. 예를 들어, 2개의 geometry가 서로 겹치는지 또는 다른 하나를 포함하는지에 대한 대답을 할 수 있어야한다. 이러한 geometry 사이의 관계, 즉 위상적 관계(topological relation)를 계산하기 위한 효율적인 알고리즘이 필요하다. 이 글에서는 오픈소스 라이브러리인 GEOS에서 어떻게 두 geometry의 관계를 확인하는지를 통해, 위상적 관계를 계산하는 알고리즘에 대해 알아보려고 한다.

GEOS에서는 두 geometry 객체의 위상적 관계를 (topologiocal relation) DE-9IM(Dimensionally Extended nine-Intersection Model)을 사용하여 표현한다. 이에 관한 설명은 OGC의 simple feature specification에 관한 문서에서 (또는 위키피디아에서) 확인할 수 있다. 따라서, GEOS에서 위상적 관계를 파악하는 함수라는 것은 결국 이 DE-9IM(이하 IM)를 계산하는 함수를 의미하고, 곧 IM을 계산하는 알고리즘을 통해 위상적 관계를 얻어내는 알고리즘을 얻을 수 있다. 다음 코드는 GEOS에서 위상적 관계를 확인하는 방법이다. 각 함수들의 구현체를 살펴보면, IM계산한 뒤 그 값을 통해 bool값을 반환하고 있는 것을 알 수 있다.

//from a GEOS test c++ code.
//test/geostest/geostest.c

GEOSGeometry* g1;
GEOSGeometry* g2;

//Query topological relations using functions.
if ( GEOSIntersects(g1, g2) ) printf("Intersect\n");
if ( GEOSDisjoint(g1, g2) ) printf("Disjoint\n");
if ( GEOSTouches(g1, g2) ) printf("Touches\n");
if ( GEOSCrosses(g1, g2) ) printf("Crosses\n");
if ( GEOSWithin(g1, g2) ) printf("Within\n");
if ( GEOSContains(g1, g2) ) printf("Contains\n");
if ( GEOSOverlaps(g1, g2) ) printf("Overlaps\n");

//Query topological relations using IM.
auto ptr = GEOSRelate(g1, g2);
if( GEOSRelatePattern(g1, g2, ptr) )

//in each function
{
    ...
    unique_ptr<IntersectionMatrix> im ( relate(g) );
    return im->~();
}

Geometry Graph

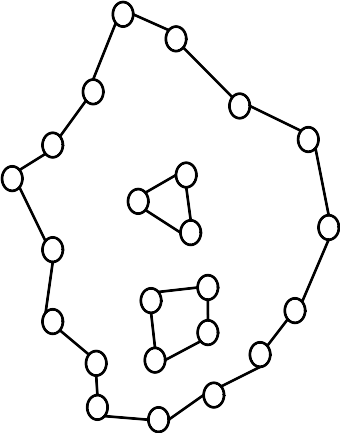
IM을 구하는 과정을 살펴보기 전에, GEOS에서 IM계산에서 사용하는 GeometryGraph클래스를 살펴보려고 한다. GeometryGraph는 geometr을 바탕으로 생성된 노드(node)와 엣지(edge)을 가지고 있는 그래프로서 각 노드와 엣지에는 (바탕이되는) geometry의 점(들)과 선(들)이 어느 위치에 있는지에 대한 위상적 관계를 저장하고 있다. 언듯 직관적으로 이해가 되지 않으므로 다음과 같은 예제를 살펴보자. 다음은 폴리곤 형식의 geometry로, 내부에 2개의 ring이 존재한다. 내부 ring 사이의 공간은 이 폴리곤에 속한다고 간주하지 않는다. (즉, exterior 이다.) GEOS (또는 기타 라이브러리)에서 폴리곤을 저장하는 방법을 떠올리면 그림의 선은 실제로 존재하지 않는다는 것을 알 수 있다. 즉, 그림에서는 점과 선으로 표현했지만, 저장한 데이터들은 점의 좌표의 배열뿐이다. 실제로는 점 사이의 선은 (메모리에) 존재하지 않고 배열에서 연속된 두 점 사이를 직선으로 잇는 것으로 생각한다. 따라서 이 폴리곤은 3개의 점의 배열들로 구성되어 있다.

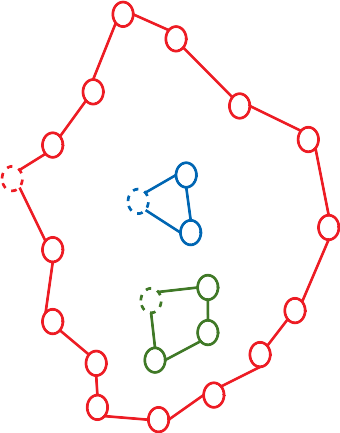
이 geometry로 생성한 GeometryGraph는 3개의 노드와 3개의 엣지로 구성되어있다. Geometry의 점들을 보고, 점의 배열을 1개의 엣지로, 점의 배열 중 몇개를 선택하여 노드로 저장한다. 다음 그림을 통해 살펴보자. 노드의 경우 그림에서 점선으로 표현한 점들이 해당한다. 엣지의 경우, 같은 색의 점들의 좌표값을 배열로 가지고 있다. 즉, 위에서 폴리곤을 나타낼 때 사용한 점의 배열마다 1개의 노드와 1개의 엣지를 생성한 것이다. 이제 각 노드 또는 엣지마다 라벨을 하나씩 가지고 있다. 빨간 선의 집합으로 인해 생성된 1개의 엣지에는 on: boundary, left: exterior, right: interior라는 라벨을 가지고 있고, 내부 링에 해당하는 파란색과 초록색으로 인해 생성된 엣지 2개는 각각 on: boundary, left: interior, right: exterior 라는 값을 가지고 있다.

 이 경우는 폴리곤의 경우였고, 라인스트링 같은 2차원 객체들은 한개의 점의 배열마다 처음 점과 마지막 점을 노드로 저장한다. 즉, 선의 양 끝점을 노드로, 전체 점의 집합을 엣지로 저장한다. 이 때, 엣지의 라벨은 on: interior이 되고 노드의 라벨은 on:boundary가 될 것이다.

Computing IM

다시 IM을 계산하기 위한 과정으로 돌아와서 GEOS의 수행과정을 살펴보자. 이 과정을 수행 해주는 클래스는 RelateOp다. RelateOp는 계산한 두 개의 geometry를 입력으로 받고 GeometryGraph을 생성한 뒤 relateComp라는 객체를 통해 IM을 계산한다. 그 후 계산한 IM을 반환하면 이 값을 통해 위상적 관계를 파악한다.

//a->relate(b) =>
//RelateOp::relate(this, other)
IntersectionMatrix*
RelateOp::relate(const Geometry *a, const Geometry *b)
{
	RelateOp relOp(a,b);
	return relOp.getIntersectionMatrix();
}

RelateOp::RelateOp(const Geometry *g0, const Geometry *g1):
	GeometryGraphOperation(g0, g1),
	relateComp(&arg)
{
}

IntersectionMatrix*
RelateOp::getIntersectionMatrix()
{
	return relateComp.computeIM();
}

따라서, IM을 계산해주는 알고리즘의 중심적인 부분을 살펴보기 위해서는 RelateComputer 클래스를 이해해야 한다.  IM을 계산하는 RelateComputer::computeIM 함수의 (간소화된) 코드는 다음과 같다.

IntersectionMatrix*
RelateComputer::computeIM()
{
    // if the Geometries don't overlap there is nothing to do
    const Envelope *e1=(*arg)[0]->getGeometry()
                ->getEnvelopeInternal();
    const Envelope *e2=(*arg)[1]->getGeometry()
                ->getEnvelopeInternal();
    if (!e1->intersects(e2)) {
        computeDisjointIM(im.get());
        return im.release();
    }

    std::unique_ptr<SegmentIntersector> si1 (
        (*arg)[0]->computeSelfNodes(&li,false)
    );
    std::unique_ptr<SegmentIntersector> si2 (
        (*arg)[1]->computeSelfNodes(&li,false)
    );

    std::unique_ptr< SegmentIntersector> intersector (
        (*arg)[0]->computeEdgeIntersections((*arg)[1], &li,false)
    );

    computeIntersectionNodes(0);
    computeIntersectionNodes(1);

    copyNodesAndLabels(0);
    copyNodesAndLabels(1);

    labelIsolatedNodes();

    computeProperIntersectionIM(intersector.get(), im.get());

    EdgeEndBuilder eeBuilder;
    std::unique_ptr< std::vector<EdgeEnd*> > ee0 (
        eeBuilder.computeEdgeEnds((*arg)[0]->getEdges())
    );
    insertEdgeEnds(ee0.get());
    std::unique_ptr< std::vector<EdgeEnd*> > ee1 (
        eeBuilder.computeEdgeEnds((*arg)[1]->getEdges())
    );

    insertEdgeEnds(ee1.get());

    labelNodeEdges();

    labelIsolatedEdges(0,1);

    labelIsolatedEdges(1,0);

    updateIM( *im );
    return im.release();
}

이제 이 코드를 파악해 보자. 먼저 두 geometry의 MBR (envelope in GEOS)이 서로 겹치지 않는다면, geometry들 끼리도 역시 아무런 위상 관계가 없다는 것은 쉽게 알 수 있다. 따라서, MBR간의 관계를 먼저 확인해본다.

const Envelope *e1=(*arg)[0]->getGeometry()->getEnvelopeInternal();
const Envelope *e2=(*arg)[1]->getGeometry()->getEnvelopeInternal();
if (!e1->intersects(e2)) {
    computeDisjointIM(im.get());
    return im.release();
}

다음은 어떤 간선 쌍이 겹치는지 확인하고 저장한다. GEOS에서는 먼저, 한 geometry 내부에서 스스로 겹치는 선이 있는지 확인한다. GeometryCollection이나 LineStirng의 경우 스스로 겹치는 선이 있을 수 있다. 이러한 경우 해당 intersection을 따로 저장한다. 다른 geometry 객체와 겹치는 부분이 아니기 때문이다. 그 다음 geometry 사이에서 겹치는 간선 쌍을 찾는다. 이 과정을 표현한 코드는 다음과 같다. Intersection에 대한 여부는 위에서 서술한 GeometryGraph에 의해 정보가 저장된다.

std::unique_ptr<SegmentIntersector> si1 (
    (*arg)[0]->computeSelfNodes(&li,false)
);
std::unique_ptr<SegmentIntersector> si2 (
    (*arg)[1]->computeSelfNodes(&li,false)
);

std::unique_ptr< SegmentIntersector> intersector (
    (*arg)[0]->computeEdgeIntersections((*arg)[1], &li,false)
);

Monotone chian sweep line algorithm

서로 겹치는 선을 찾을 때는 brute force를 사용하여 (모든 선 쌍들을 비교하는 알고리즘인) quadratic time algorithm을 사용할 수 도 있다. 그렇지만 좀 더 효율적인 계산을 위해 GEOS에서는 기본적으로 monotone-chain sweep line algorithm을 사용한다. 이 과정에서 위에서 서술한 GeometryGraph를 사용한다. 알고리즘에 대한 이론적인 설명은 다음 논문에서 확인할 수 있다. (링크) GEOS에서 사용하는 monotone-chain과는 약간 다르지만, 핵심이 되는 내용은 다음과 같다. Chain (polygonal chain)은 연결된 선의 집합이다. Monotone chain도 역시 chain의 일종으로 선의 집합으로 구성되어있다. 중요한 포인트는 monotone chain속의 선들은 서로 겹치지 않는다는 것이다. 이를 바탕으로 하면, 모든 선들을 monotone chain으로 구성하고 monotone chain사이에 intersection이 있는지 확인하면 더 효율적으로 찾을 수 있다. 논문에 따른 수학적인 monotone chain의 정의는 다음과 같다.

어떤 chain C 어떤 선 L에 수직인 모든 선 L0에 대해 교점이 최대 1개이면, 그 chain C는 선 L에 대해 monotone 이다. (A chain C is monotone w.r.t L if there is at most one intersection point between C and all lines L0 s.t. L0 is perpendicular to L.)

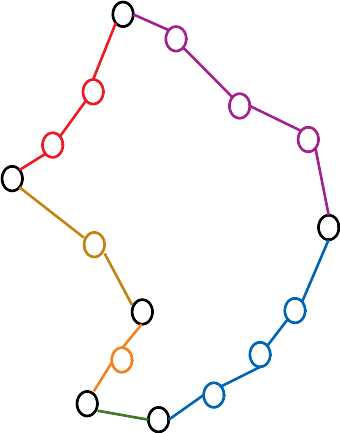
GEOS에서는 약간 속성을 바꾸어 monotone chain을 다르게 정의하였다. 다른 정의에 따르면 한 개의 monotone chain 속의 모든 선이 서로 겹치지 않는 것은 물론 양 끝 선의 끝 점으로 이루어진 MBR (envelope) 속에 모든 선이 속한다. 따라서, 2개의 monotone chain이 있을 때 MBR의 비교를 통해 더 빨리 intersection을 찾을 수 있을 것이다. 이를 위해 GEOS는 다음과 같은 방법으로 monotone chain을 구성한다. 아래 그림에서 같은 색의 점들이 한 monotone chain에 속한다. 색이 칠해져 있지 않는 점들은 양 쪽의 monotone chain에 속하는 것이다. 즉, 빨간색과 보라색 monotone chain은 1개의 점을 공유한다.

이제, Monotone chain을 바탕으로 sweep line algorithm을 통해 intersection을 찾는다. 일반적으로 x축으로 정렬을 하고, x축에 수직인 선(sweep line)을 긋고 이와 겹치는 객체들 (여기서는 monotone chain) 사이에서만 intersection을 찾는다. 각 점의 x좌표에 해당하는 점에 대해서만 선을 그으면 된다는 점은 쉽게 도출해 낼 수 있다. Monotone chain을 사용할 경우, 각 chain의 시작점과 끝점의 x좌표를 사용하여 현재 sweep line과 겹치는 monotone chain의 집합을 쉽게 유지할 수 있다. GEOS에는 이 정보를 event형태로 관리한다. Monotone chain의 시작점을 기준으로 insert event를 삽입하고 끝점을 기준으로 delete event를 사용한다.

Computing IM (continued)

이제 코드로 돌아와서 어떻게 위 알고리즘을 사용했는지 알아보자.

unique_ptr<EdgeSetIntersector> esi(createEdgeSetIntersector());

typedef vector<Edge*> EC;

EC self_edges_copy;
EC other_edges_copy;

EC *se = edges;
EC *oe = g->edges;
if ( env && ! env->covers(parentGeom->getEnvelopeInternal()) ) {
    collect_intersecting_edges(env, se->begin(), se->end(), self_edges_copy);
    se = &self_edges_copy;
}
if ( env && ! env->covers(g->parentGeom->getEnvelopeInternal()) ) {
    collect_intersecting_edges(env, oe->begin(), oe->end(), other_edges_copy);
    oe = &other_edges_copy;
}
esi->computeIntersections(se, oe, si);

여기서, EdgeSetInetersector를 통해 계산하는 것을 확인할 수 있다. EdgeSetIntersector는 intersection을 찾는 알고리즘의 추상화 클래스로, GEOS에서는 현재 위에 설명한 monotone chain sweep line algorithm 을 구현한 SimpleMCSweepLineIntersector를 사용하고 있다. 해당 코드에 대한 내용은 이 글에서는 생략한다. 교점(의 후보)을 찾는다면, (monotone chain algorithm이 선 2개를 반환하여) 이를 LineIntersector에 입력하여 해당 교점이 어떤 교점인지 확인한다. 3가지 경우의 수가 있다. 만나지 않거나, (입력된 두 선분의 끝점이 아닌) 1개의 교점을 갖거나 또는 두 선분이 겹치는 경우가 있다. 이 중 1개의 교점을 갖는 경우 proper하다고 한다. 이 때, 그 1개의 교점이 각 geometry의 boundary가 아닐 경우, properInterior 플래그를 추가로 설정한다.

이러한 정보를 바탕으로 IM값을 결정한다. 각 geometry의 차원, proper 여부 그리고 properInterior 여부가 중요하다. 해당 코드는 다음과 같다.

int dimA=(*arg)[0]->getGeometry()->getDimension();
int dimB=(*arg)[1]->getGeometry()->getDimension();
bool hasProper=intersector->hasProperIntersection();
bool hasProperInterior=intersector->hasProperInteriorIntersection();

if (dimA==2 && dimB==2) {
    if (hasProper) imX->setAtLeast("212101212");
} else if (dimA==2 && dimB==1) {
    if (hasProper) imX->setAtLeast("FFF0FFFF2");
    if (hasProperInterior) imX->setAtLeast("1FFFFF1FF");
} else if (dimA==1 && dimB==2) {
    if (hasProper) imX->setAtLeast("F0FFFFFF2");
    if (hasProperInterior) imX->setAtLeast("1F1FFFFFF");
} else if (dimA==1 && dimB==1) {
    if (hasProperInterior) imX->setAtLeast("0FFFFFFFF");
}

그러나 아직 끝이 아니다. 위에서 찾는 교점은 두 선분의 끝점을 고려하지 않았으므로, 이를 고려해야 한다. 이런 경우 proper한 교점을 찾는 것은 아니지만, 해당 교점을 GeometryGrah의 엣지 값에 매달아 놓게 된다.

(Will be continued)